Supervised Learning and Kernel Regression In
supervised learning, we seek to learn to predict a target variable from
data. The way this
happens is by having access to a number of data vectors with their
associated targets (i.e. labels or physical measurements), defining
some functional form that maps data to targets, and a merit criterion
which is small when estimates are close to targets. One salient
question for this domain is how to choose the functional form such that
the resulting optimization problem is solvable, but sufficiently
general so as to be able to capture important relationships between
data and targets. In this thread of research, we investigate how to
manage this tradeoff for the case that estimators belong to a
Reproducing Kernel Hilbert Space (RKHS), which yields a very rich class
of estimators. However, owing to the Representer Theorem, this choice
also makes the complexity of the optimization problem comparable to the
training sample size, which is untenable for streaming applications or
large-scale problems. However, by carefully constructing subspaces onto
which we project RKHS-valued stochastic gradient algorithms, we are
able to find optimally compressed kernelized regression functions. This
is in contrast to a long history of literature trying to ameliorate the
complexity growth of kernel methods with the training sample size that
typically violate the optimality properties of the iterative sequences
to which they’re applied.
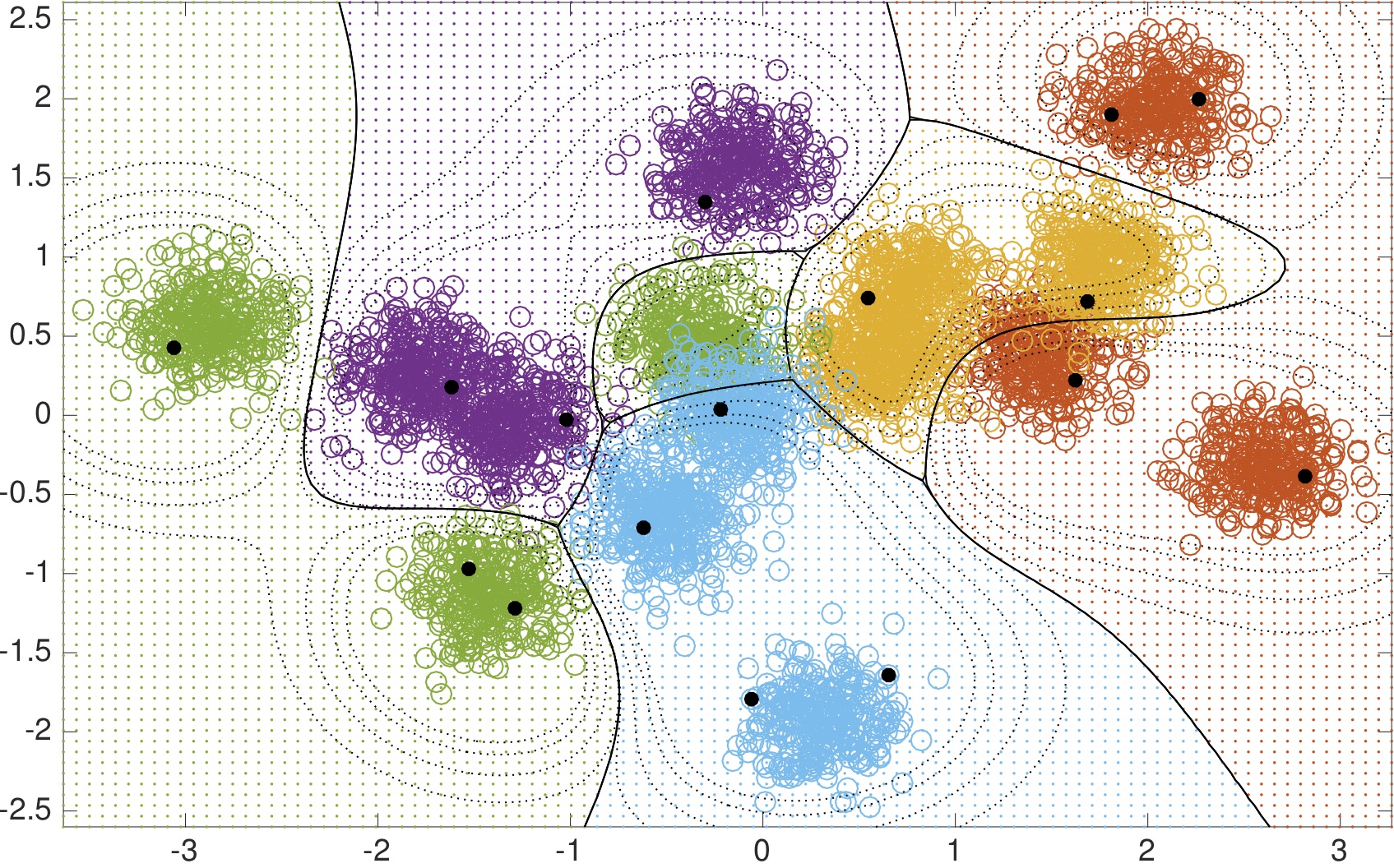
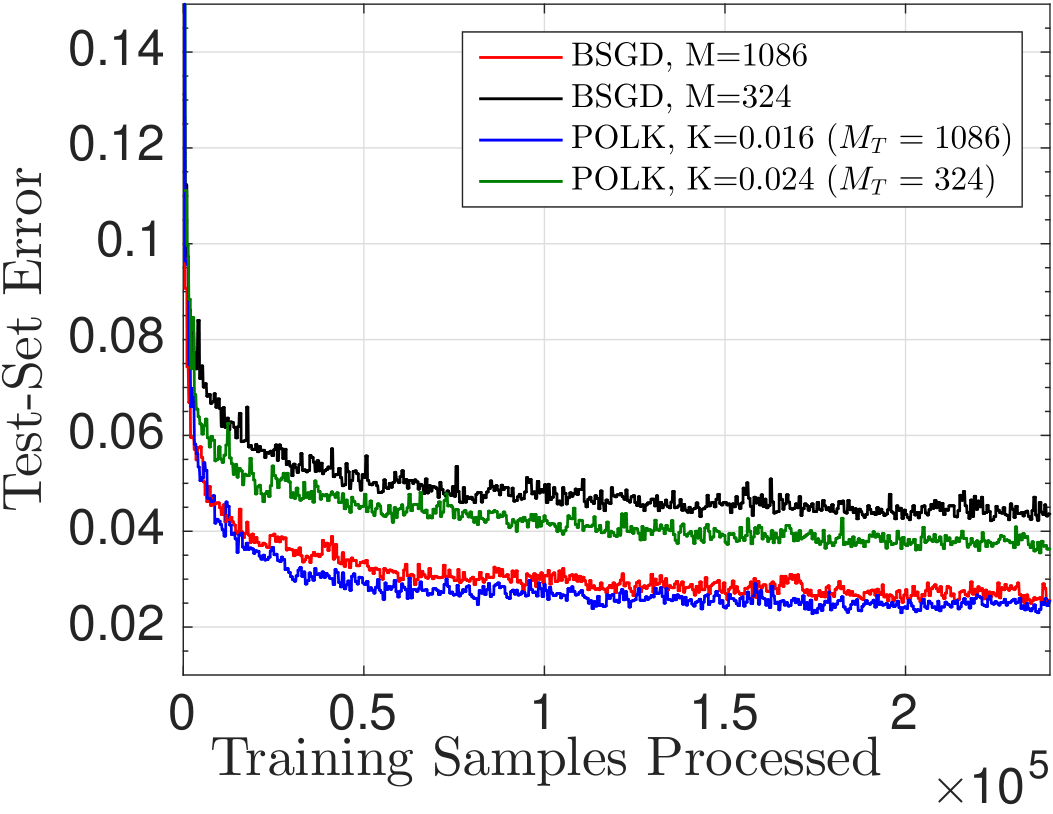
We call this method Parsimonious Online
Learning with Kernels (POLK), and illustrate a couple examples of the
decision surface defined by POLK when used with a Gaussian kernel for
two-dimensional multi-class classification. On the left we visualize
the surface defined by kernel logistic regression; on the right a
kernel support vector machine classifier is visualized. [Video]
These results are explained in detail in the following journal paper:
A. Koppel, G. Warnell, E. Stump, and A. Ribeiro, “Parsimonious Online
Learning with Kernels via Sparse Projections in Function Space,” in
Journal of Machine Learning Research
(under review), Nov. 2016
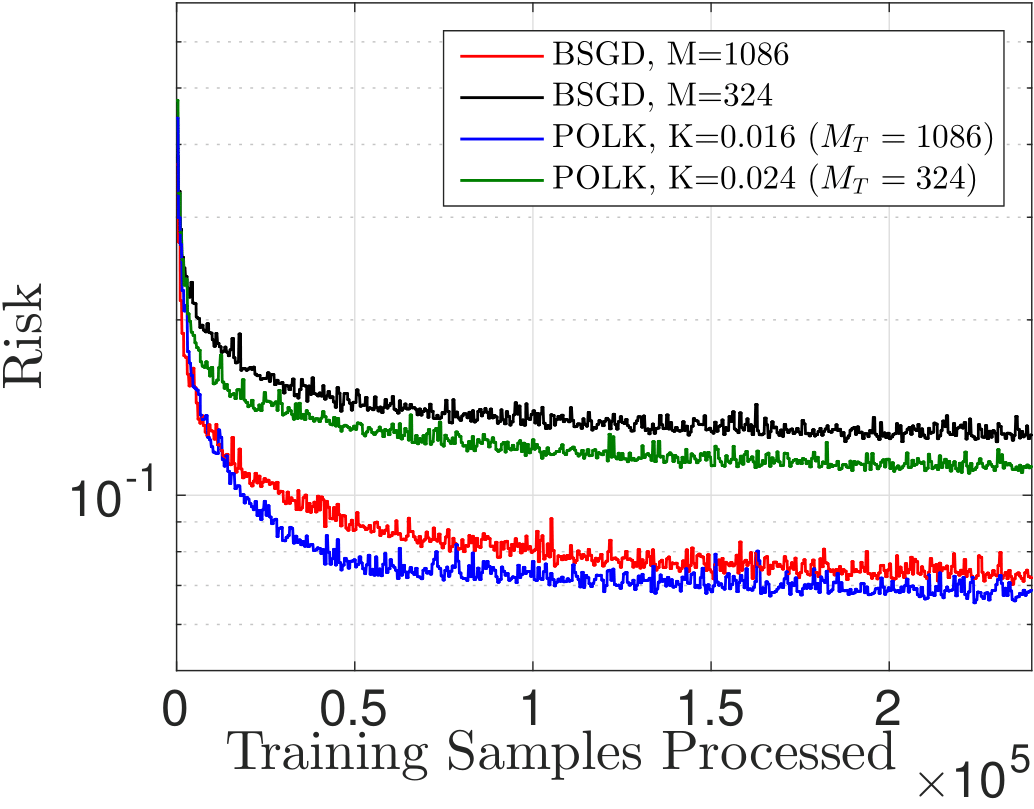
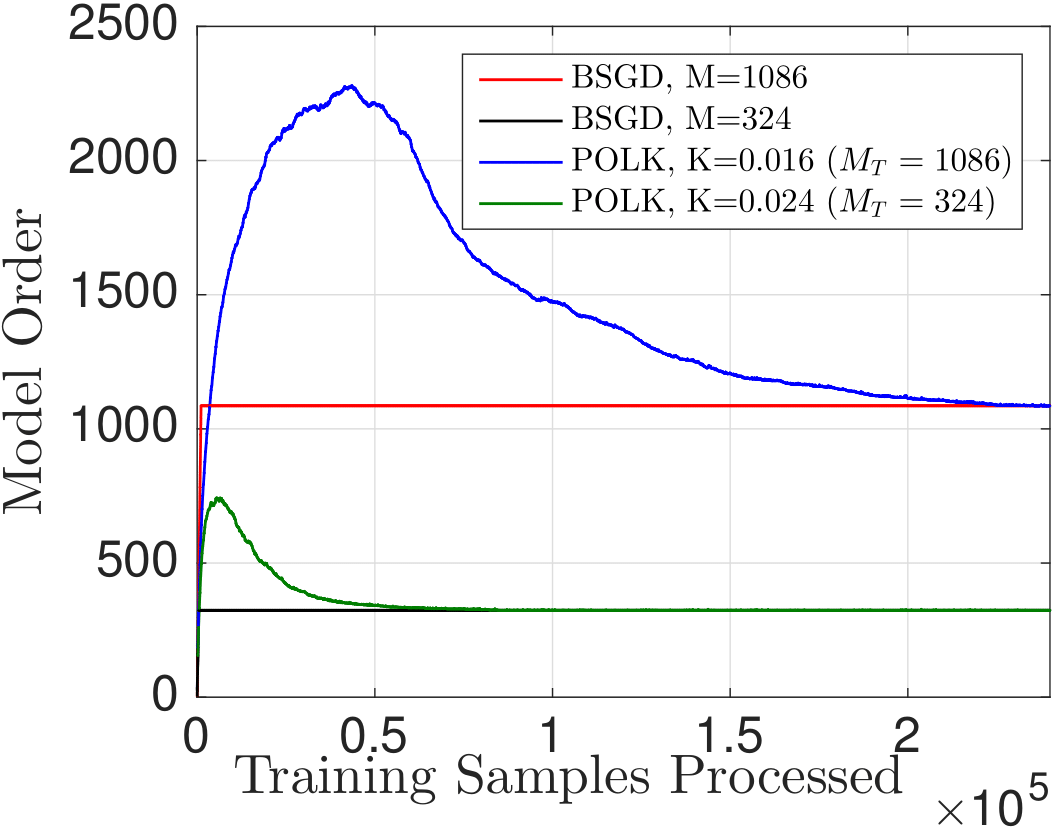
The
way this optimal compression works contrasts with existing approaches:
typically, one fixes the memory required and projects all subsequent
points onto a subspace of fixed size. But this may cause divergence. By
contrast, by allowing the model complexity to be flexible and dependent
on informativeness according to the RKHS norm, we can tie gradient
projections to memory-reduction, and ensure both near-optimality and
finite memory (depending on the choice of kernel bandwidth, step-size,
and compression budget). We can observe this phenomenon in the figures
below.
Risk-Aware Learning We have recently investigated how this framework can be extended to overcome outliers and ill-conditioned data in streaming scenarios. We propose to do so through replacing the standard supervised learning objective by one that incorporates a dispersion statistic, which can be mathematically encapsulated by coherent risk. Coherent risk is a concept from operations research/mathematical finance which quantifies the uncertainty in a decision.
To
date, risk has not been used in nonparametric estimation. There are two
ways to modify online supervised learning procedures to overcome
outliers and become risk-aware. One would be to add the risk function
as a penalty term to the objective. The motivation fo this formulation
can be connected directly from the bias-variance
(estimation-approximation) tradeoff in machine learning. Minimizing
risk functions, however, requires addressing the fact that they have a
structural form where there are two nested expectations in the
objective, and hence the stochastic gradient method inside POLK must be
replaced with stochastic quasi-gradient (SQG) method. The use of SQG
together with the subspace projections of POLK, their convergence, and
experimental gains, is the subject of a recent submission to IEEE TSP.
Amrit S. Bedi, A. Koppel, and K. Rajawat. " Nonparametric Compositional
Stochastic Optimization " in IEEE Trans. Signal Processing (submitted),
Feb. 2019
Alternatively,
one may write the risk function as a nonlinear constraint. However, to
come up with kernelized learning algorithms, one must first extend the
Representer Theorem to cases with constraints. We propose this
extension, and then upon this foundation we develop a primal-dual
method for solving the constrained optimization problem in function
space. This formulation is equally applicable to risk-aware learning
and model predictive control with obstacle-avoidance constraints. These
contributions are summarized in the paper:
A. Koppel, K. Zhang, H. Zhu, and T. M. Baser. ”Projected Stochastic
Primal-Dual Method
for Constrained Online Learning with Kernels” in IEEE Trans. Signal
Process. (submitted),
Apr. 2018.
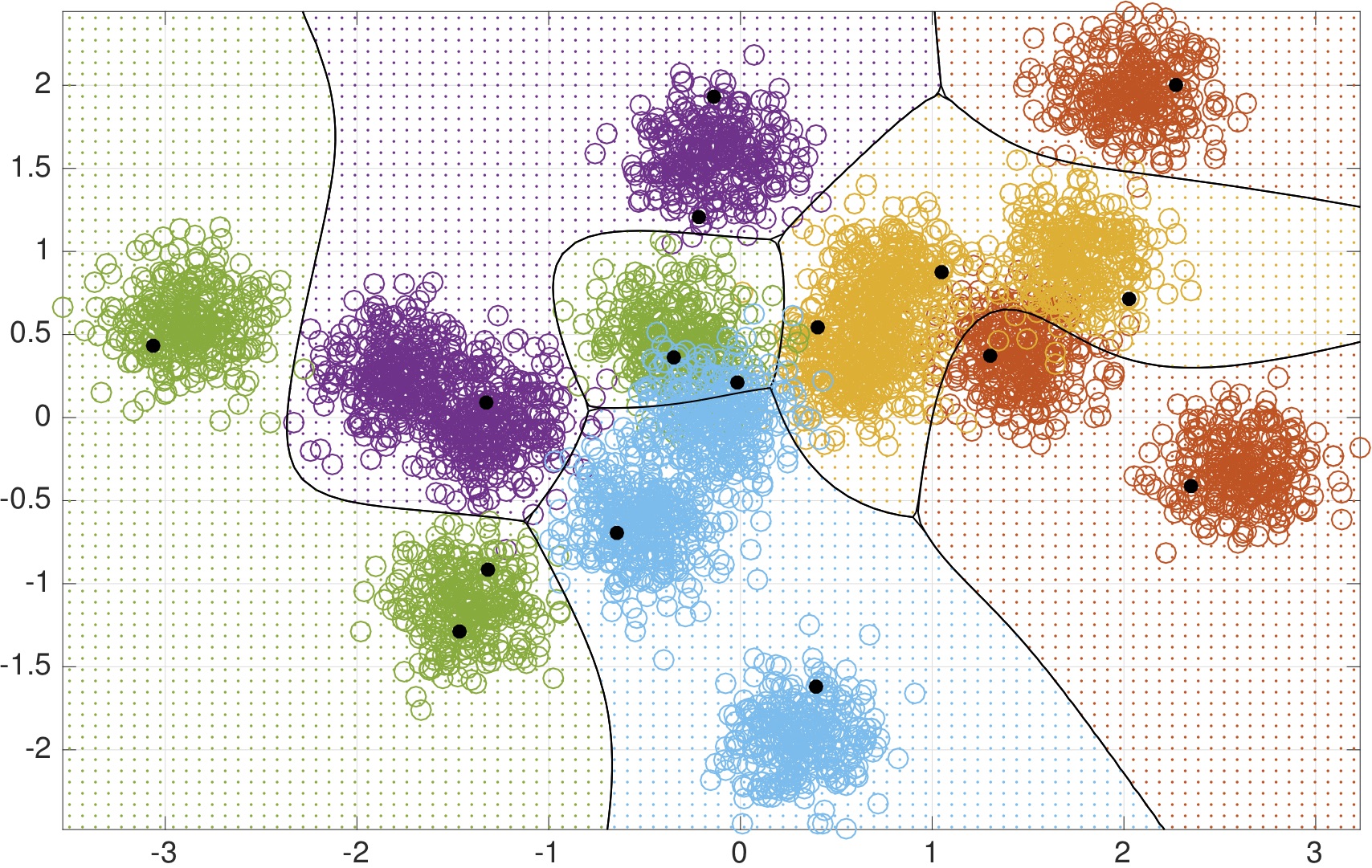
In the following plot, we display how a canonical risk function, called
conditional value at risk, changes the decision surface and model
complexity of a nonparametric estimator, for the cartoon data set we
display above.
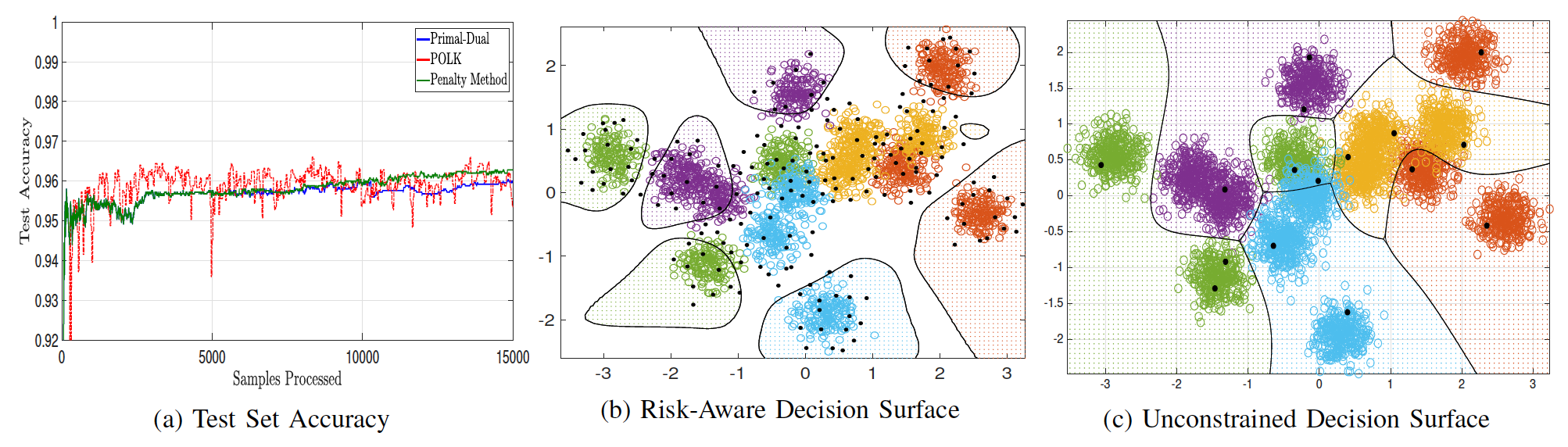
Here we display how these methods work for an online kernel SVM classifier with optimal memory-reduction. On the left, we place test set accuracy for this synthetic Gaussian mixture point cloud for primal-dual method, the new innovation here, as compared with its unconstrained variant (POLK) and an approximate penalty method. In the middle and right plot, when risk-constraints are enforced, then confidence regions are only drawn far from regions of class overlap. Moreover, the estimator tracks both the median of the distribution as well as its spread. This happens because the loss function now penalizes uncertainty in the decisions. Therefore, by ensuring risk is constrained, classifications are still made correctly but are aware of uncertainty regions.
In
reinforcement learning, an autonomous agent observes a sequence
of rewards as it traverses its environment based upon the actions it
takes. Depending on which actions it takes, it may end up in more or
less rewarding states. The question is how to choose the policy, i.e.,
the map from states to actions, so as to ensure the long-run
(discounted) accumulation of rewards is maximized. This long-run
accumulation is called the value. Methods for reinforcement learning
roughly cluster into two classes, each of which come with their own
benefits and drawbacks. On the one hand, it is possible parameterize
the policy as a specific form, and then to run versions of stochastic
gradient ascent directly on the value function using a classical
representation of the value function's gradient called the Policy
Gradient Theorem. Doing so is called Policy Search, and for general
continuous spaces is intimately tied with non-convex stochastic
optimization. On the other hand is approximate dynamic programming
(ADP), in which one writes the optimal value function starting from one
state as the expected optimal value function starting from another plus
the one-step reward, a recursion known as Bellman's equation. Bellman's
equations are stochastic fixed point recursions whose convergence is
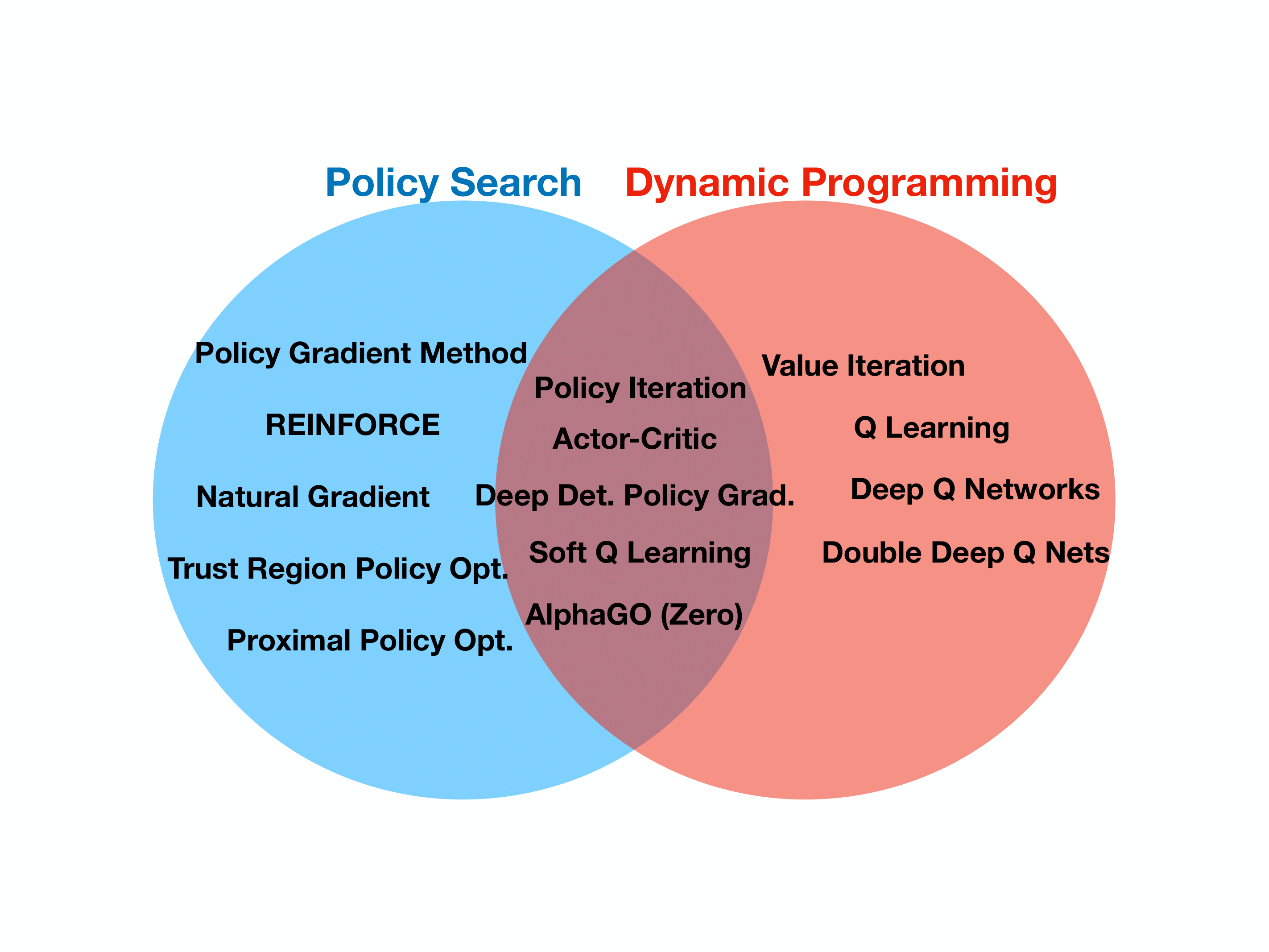
delicate in the face of different value function parameterizations. My
attempt at organizing works on this topic is given in the following
Venn diagram -- note that several successful recent works are situated
in the intersection of APD and Policy Search.
Convergent APD with Nonlinear Function Approximation via
Compressed Kernel Methods
Approximate dynamic programming (ADP), at its core, relies on Bellman's
equations, where we write the value starting from one state as the
expected value starting from another plus the one-step reward. Then, to
solve for the (optimal) value function, we have to solve this fixed
point equation through stochastic approximation. Thus, many classical
techniques for RL use stochastic fixed
point iterations, e.g., Temporal Difference Learning and Q Learning.
These methods break down when combined with function approximation
(parameterization),
however, which is intrinsically required for continuous Markov Decision
Problems. My approach to mitigating these issues is to reformulate the
fixed point problems defined by Bellman’s evaluation into compositional
optimization problems, and then parameterizing the value function as
one that belongs to a reproducing Kernel Hilbert
space. Then, by combining the kernel parameterization with specific
optimization tools for compositional settings, i.e., stochastic
quasi-gradient methods, and a projection step that ensures the
complexity of the kernel representation does not become unwieldy, we
can have globally convergent ADP that uses nonlinear function
approximators of moderate complexity.
See an example of how this works on the Mountain Car domain in the
below plot, where we
should that the Bellman error converges and we obtain a
memory-efficient value function that is transparently interpretable in
the contour plot. Here the value function is simply a weighted
combination of some kernel evaluations at past state-action pairs. We
handle the growth of the kernel parameterization through sparse
subspace projections in a manner very similar to POLK.
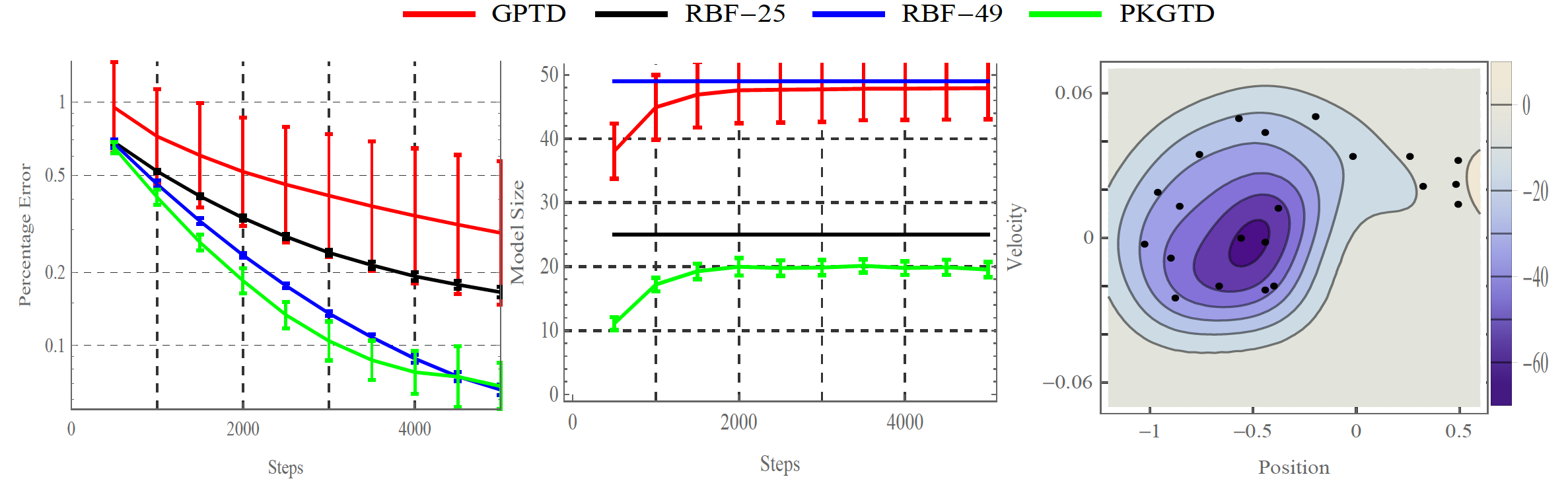
These results are explained in detail in the following journal paper:
A. Koppel, G. Warnell, E. Stump, P. Stone, and A. Ribeiro. “Policy
Evaluation in Continuous MDPs with Efficient Kernelized Gradient
Temporal Difference,” in IEEE Trans. Automatic Control (submitted),
Dec. 2017.
This approach may be adapted to solve the Bellman optimality
equation for action-value functions. In the below left contour plot we
show how
this may be used to solve the Continuous Mountain car and obtain
interpretable results. On the left below, the
value function associated with the learned policy that is obtained by
maximizing the action-value function. On the right we plot the
resulting policy.
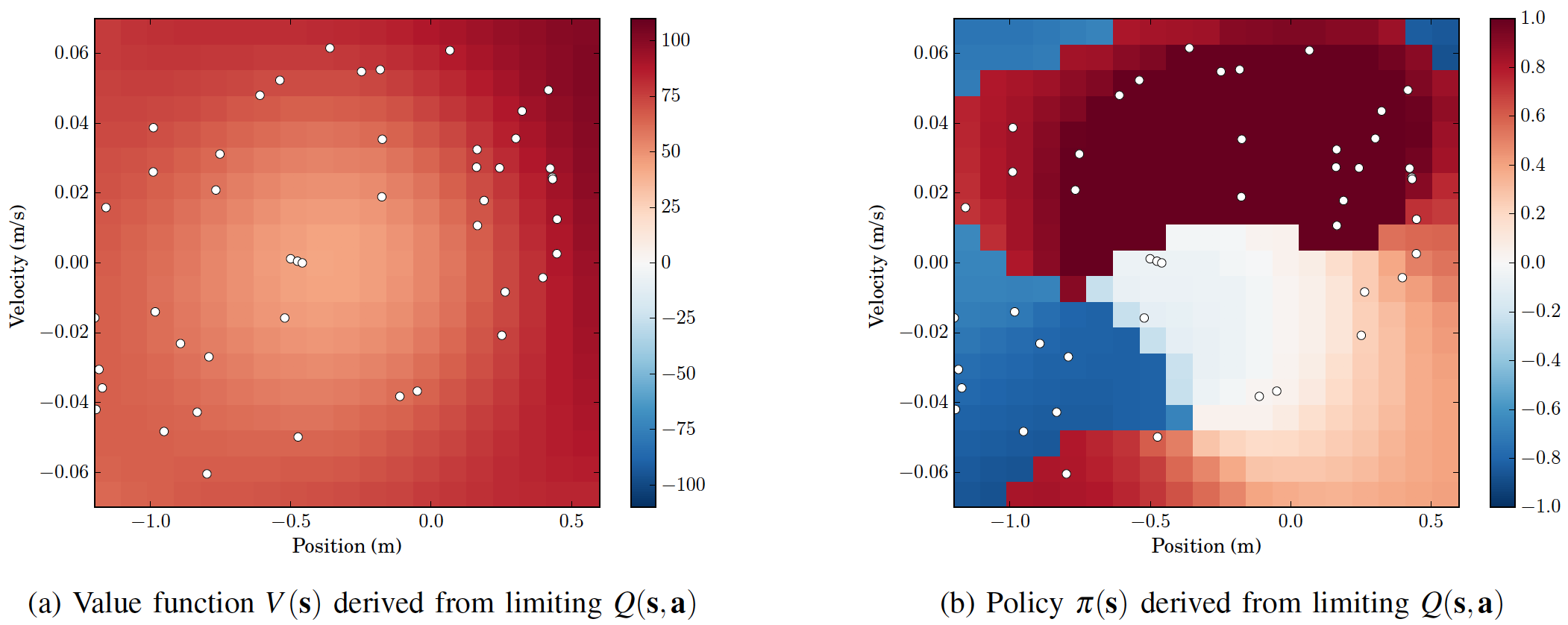
These results are explained in detail in the following journal paper:
A. Koppel, E. Tolstaya, E. Stump, and A. Ribeiro. ”Nonparametric
Stochastic Compositional
Gradient Descent for Q-Learning in Continuous Markov Decision Problems”
in IEEE
Trans. Automatic Control (to appear), 2019.
The main questions cracked open by these works is how to overcome the
need for smoothness in the function approximation through the necessity
of Lipschitz gradients, due to the fact that Bellman's optimality
equation is non-smooth: the presence of the maximum and the fact that
the reward are non-smooth are intrinsic to the problem setting.
Moreover, reformulating the problem as a compositional problem yields a
significantly slower learning rate than stochastic fixed point methods.
Are their alternative reformulations that attain mean convergence rates
comparable to usual TD or Q learning?
Improving the Reliability of Policy Search Policy
gradient methods are the building block of many canonical reinforcement
learning schemes due to their ability to scale gracefully to continuous
spaces (they avoid the need to maximize the Q function in the inner
loop of the algorithm) as compared with approximate dynamic
programming. However, their performance is typically high variance, due
to the fact their search directions are biased and high variance. Over
the past year, I've been studying ways to improve the limiting behavior
and variance of such methods.
More specifically, in several canonical references on policy gradient
in the infinite horizon setting, authors claim that these first-order
stochastic methods converge to local maxima of the value function.
However, given that the setting is a non-convex stochastic program,
these claims are faulty. Moreover, the finite time performance of PG
methods are unknown. This is because obtaining unbiased estimates of PG
requires unbiased estimates of the policy gradient. We proposed a way
to obtain such estimates based on random horizon rollouts for the Q
function, which permits i.i.d. sampling from the correct distribution,
which we call Random Policy Gradient (RPG) At the end of the day, this
allows us to establish conditions under which PG methods converge to
stationarity and derived for the first time its iteration complexity,
demonstrating PG method behaves similarly to classical behavior of
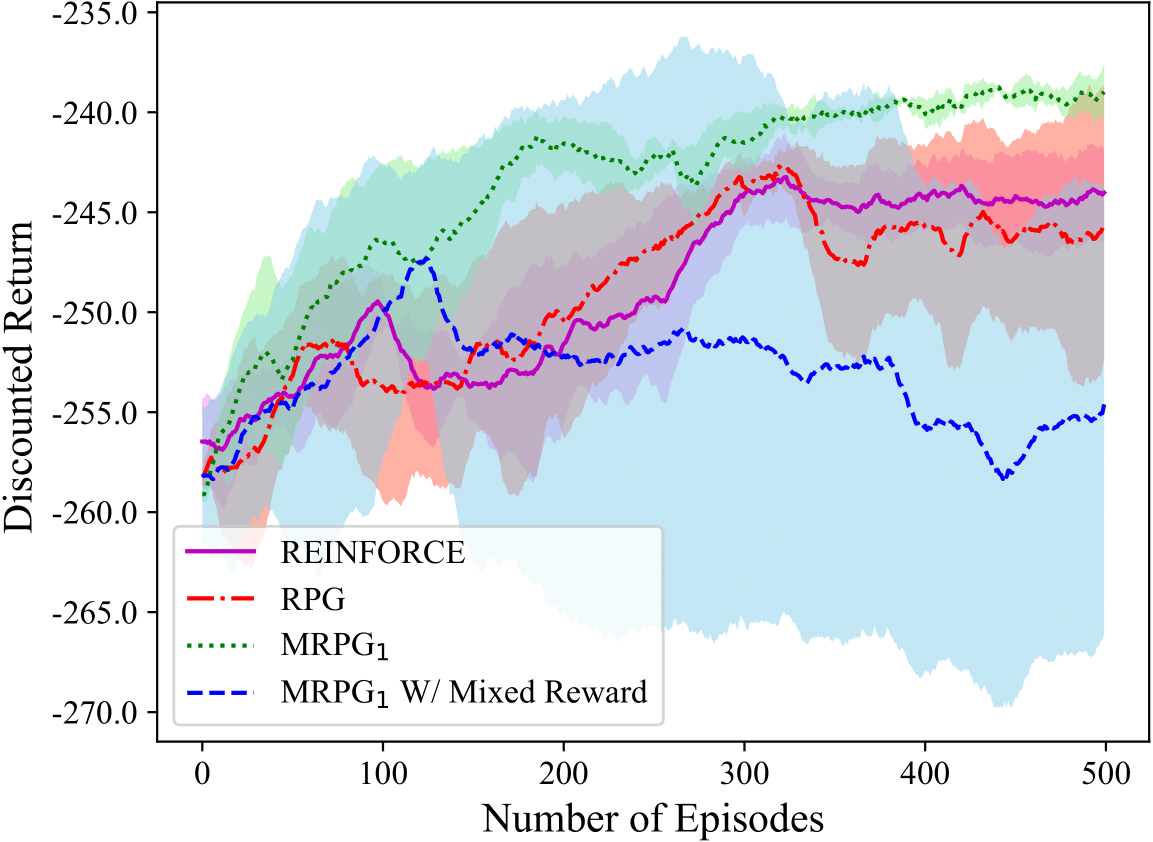
stochastic gradient method in non-convex settings. The figures to the
right show that in an implementation of RPG as compared to REINFORCE on
the inverted pendulum, the gradient norm of the objective behaves
similar to non-convex stochastic gradient method, and yields more
consistent policy improvement. These results are detailed in the
following paper:
Thus, in a recent work, we established conditions under which PG
methods converge to
stationarity and derived for the first time their iteration complexity:
K. Zhang, A. Koppel, H. Zhu, T. Basar, “Convergence and Iteration
Complexity of Policy Gradient Methods for Infinite-horizon
Reinforcement Learning,” in IEEE Conference on Decision and Control
(submitted), Nice, France, Dec. 11-13, 2019.
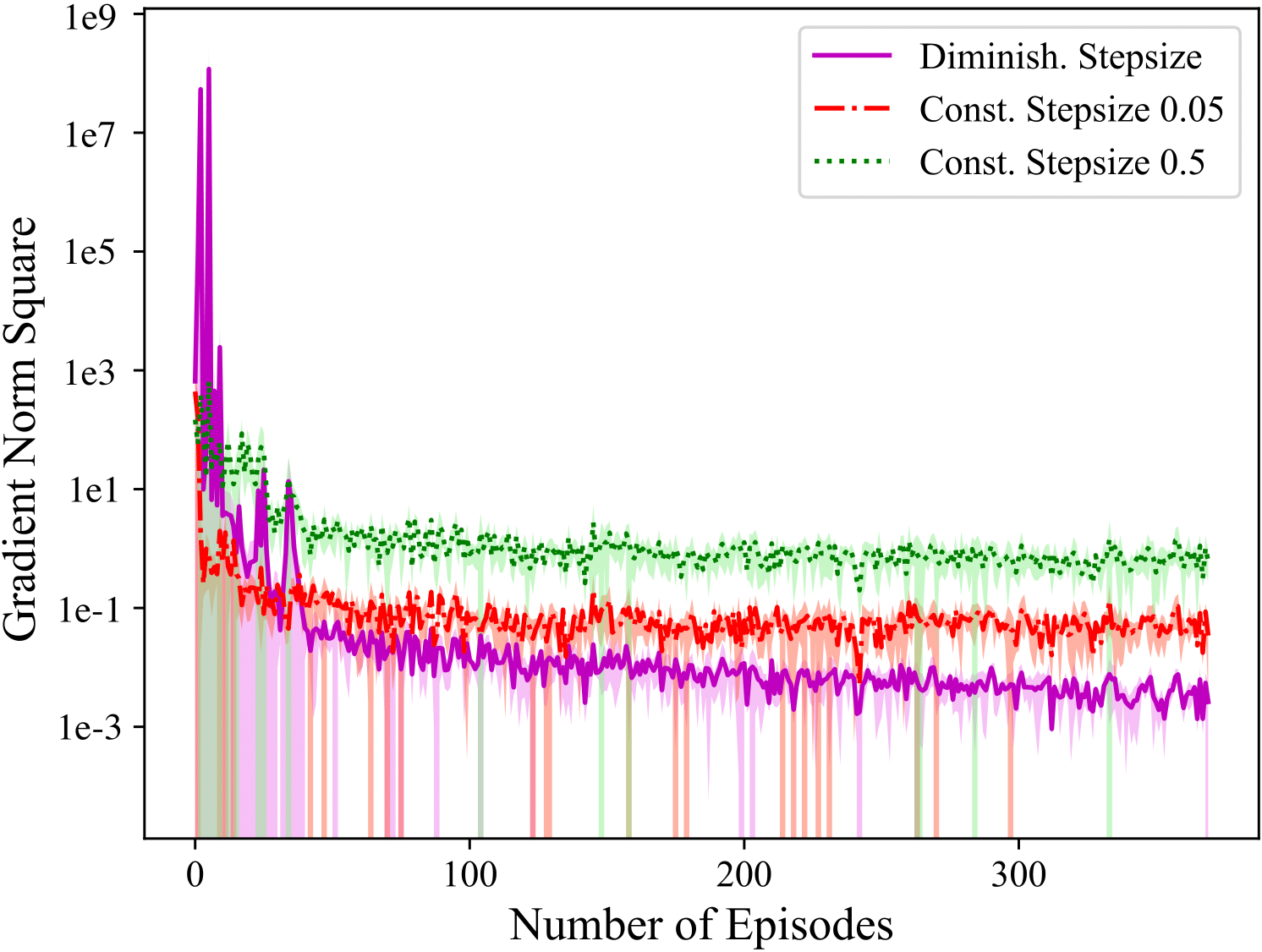
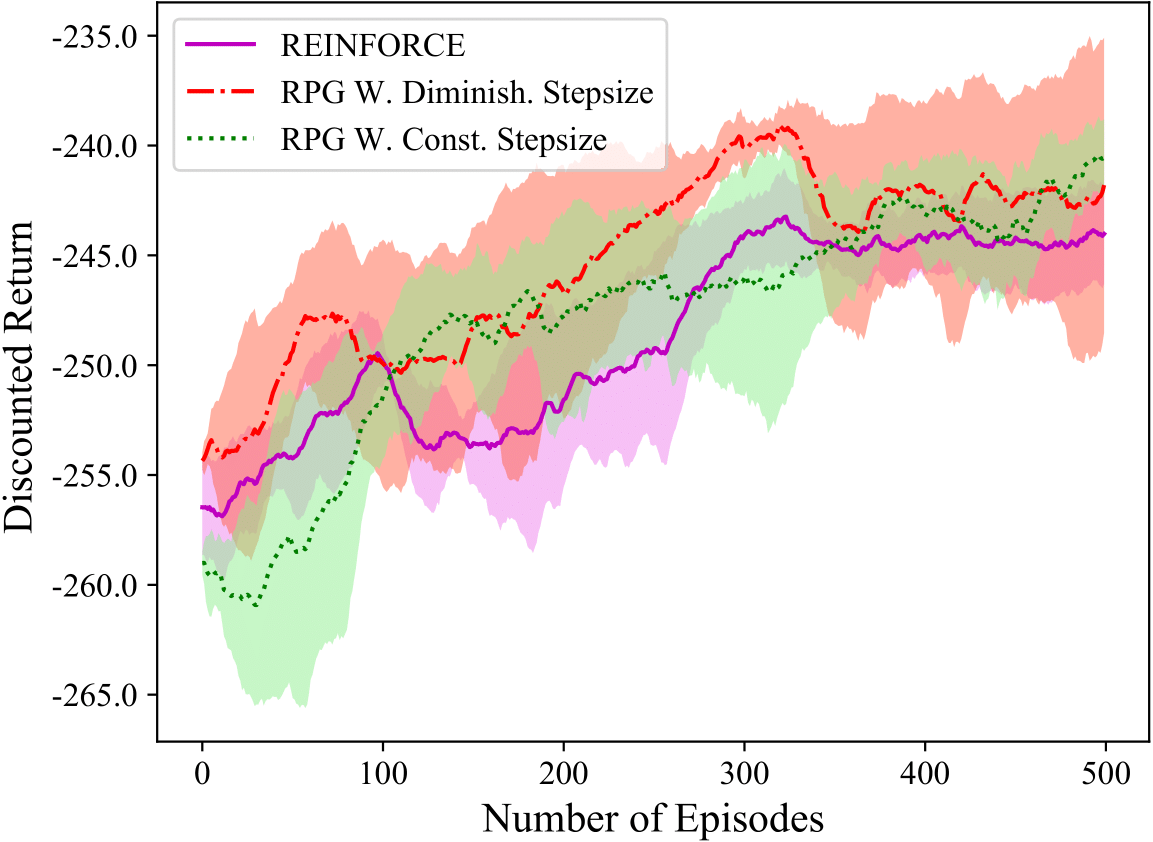
These results then motivate us investigating whether one can exploit
recent advances in non-convex optimization to design improved policy
search routines. Thus, we characterize conditions that yield
convergence to approximate local maxima (second-order stationarity
points) through a combination of modified step-size rules and
additional hypotheses on the reward and policy parameterization.
Specifically, when the policy parameterization has positive definition
Fischer information, and the reward function's absolute value is
strictly lower bounded away from null, policy gradient method can
escape saddle points efficiently, and hence converge to approximate
local extrema. The bolded condition should be interpreted as saying
it's better to always provide constructive criticism to an RL agent,
i.e., ``you get more bees with honey." These results are detailed
in the upcoming submission:
K. Zhang, A. Koppel, H. Zhu, and T. M. Baser. "Global Convergence of
Policy Gradient Methods: A Nonconvex Optimization Perspective" in SIAM
Journal on Control and Optimization (submitted), Jan. 2019.
Experimentally, while we observe that these modified step-size rules
combined with reward offsets to ensure positivity yield enhanced policy
improvement, their sample path variance is still quite large. This
corroborates recent experimental evidence from Joelle Pineau from FAIR
Montreal/McGill who has experimentally analyzed several deep
reinforcement learning schemes and pointed out how irreproducible their
results are. This is theoretically substantiated by the fact that in
the POMDP literature, it's established that the variance of estimating
a policy gradient using a score function, when following a trajectory,
is proportional to the length of the trajectory.
To sidestep this bottleneck, we proposed a way to modify the classic
the Policy Gradient Theorem such that the score function does not
appear. In particular, we propose computing the gradient of the value
function with respect to the policy using the Hahn-Jordan decomposition
of signed measures. Doing so yields the fact that the policy gradient
is a difference of two policy measures: a positive part and a negative
part. In the POMDP literature, this is called weak-derivative gradient
estimation. With this alternative way of writing the PG Theorem, we
then derive stochastic gradient based schemes and establish their
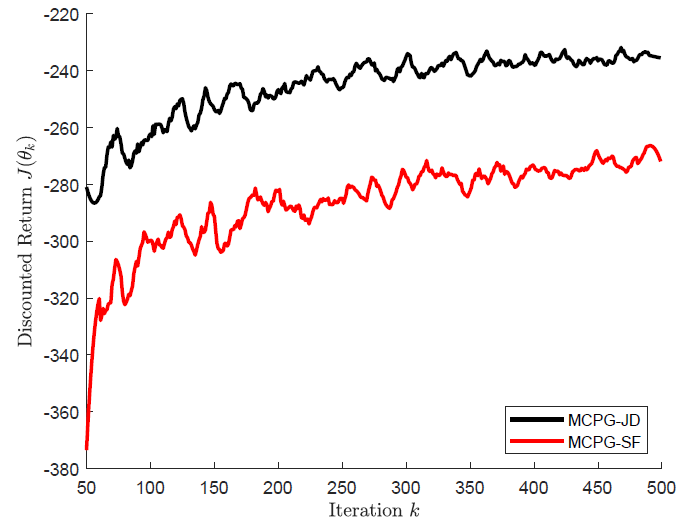
convergence. More interestingly, for the Gaussian policy, we establish
that the policy gradient estimate is provably lower variance, and hence
yields accelerated convergence, as may be observed experimentally in
the follwing evaluation on Pendulum, where we compare with the score
function-based policy gradient. These
results are formalized in the following submission:
S. Bhatt, A. Koppel, V Krishnamurthy, “Policy Gradient using Weak
Derivatives for Reinforcement Learning,” in IEEE Conference on Decision
and Control (submitted), Nice, France, Dec. 11-13, 2019.
In
standard inference techniques, we learn parameters of a statistical
model or control policy that maps features to a target, i.e., binary
label or action. This is the case with usual formulations of
regression, classification, and reinforcement learning/learning
control. By contrast, in Bayesian methods, we use past observations, a
measurement model, and a prior, together with Bayes' Rule, to construct
an entire distribution over outcomes for the present unknown. Keeping
track of an entire posterior distribution, rather than a point
estimate, allows one to design systems based on quantities more than
just the average outcome, such as higher-order moments or quantiles,
which are important for, e.g., reliability or safety guarantees.
Of course, if one restricts focus to just the posterior mean and
hypothesizes a linear measurement model with additive white noise, then
a Kalman filter tracks the required information. When such linear
dynamics and simple noise assumptions are invalid, nonparametric
Bayesian methods such as Gaussian Processes and Monte Carlo allow one
to estimate parameters of an arbitrary posterior distribution. However,
doing so when observations (or Monte Carlo particles) arrive in
sequential fashion or their total number is infinite, has unbounded
complexity. This issue is known as the curse of dimensionality in
nonparametric statistics. Thus, to enable tracking of arbitrary
posterior distributions in the online setting, one requires
consistency-preserving compression routines. While many compression
tools exist, their formal statistical properties are often poorly
understood, and thus it is difficult to evaluate them beyond numerical
experimentation.
Gaussian Processes Gaussian processes are a framework
for hypothesizing
a Gaussian distribution over function spaces, and permit restricting
focus to only computations involving the posterior mean and covariance.
Unfortunately, computing the posterior mean and covariance has
complexity cubic in the sample size, and hence in the online setting
grows unbounded as time progresses. Memory reduction techniques rely on
numerous approximations: approximating the kernel matrix, projecting a
growing collection of data points onto the likelihood of another, or
approximating the Gaussian likelihood using variational upper bounds.
The merits and drawbacks of these approaches is an active area of
research -- see Chapter 8 of the famous GP textbook for a nice
numerical evaluation of existing approaches.
From a statistical perspective, the merit of a memory-reduction
technique for GPs should
be in how close to statistical consistency it becomes as the number of
training examples becomes large. This is the metric of optimality in
Bayesian statistics. Motivated by this fact, in the following paper, we
propose a greedy forward selection technique for memory reduction of
Gaussian processes based on a metric between distributions called the
Hellinger metric. The reason for this selection is that it (1) can be
computed in closed-form for Gaussian distributions; and (2) many
existing statistical consistency results for GPs from the statistics
literature are expressed in terms of it. A key contrast of this
approach is that we do not fix the number of kernel covariance elements
(also known as pseudo/inducing inputs) in advance, but instead allow
the number to flexibly grow or shrink as new training examples arrive.
As a result, we can mathematically establish that the memory-reduced GP
yields a posterior that is nearly consistent.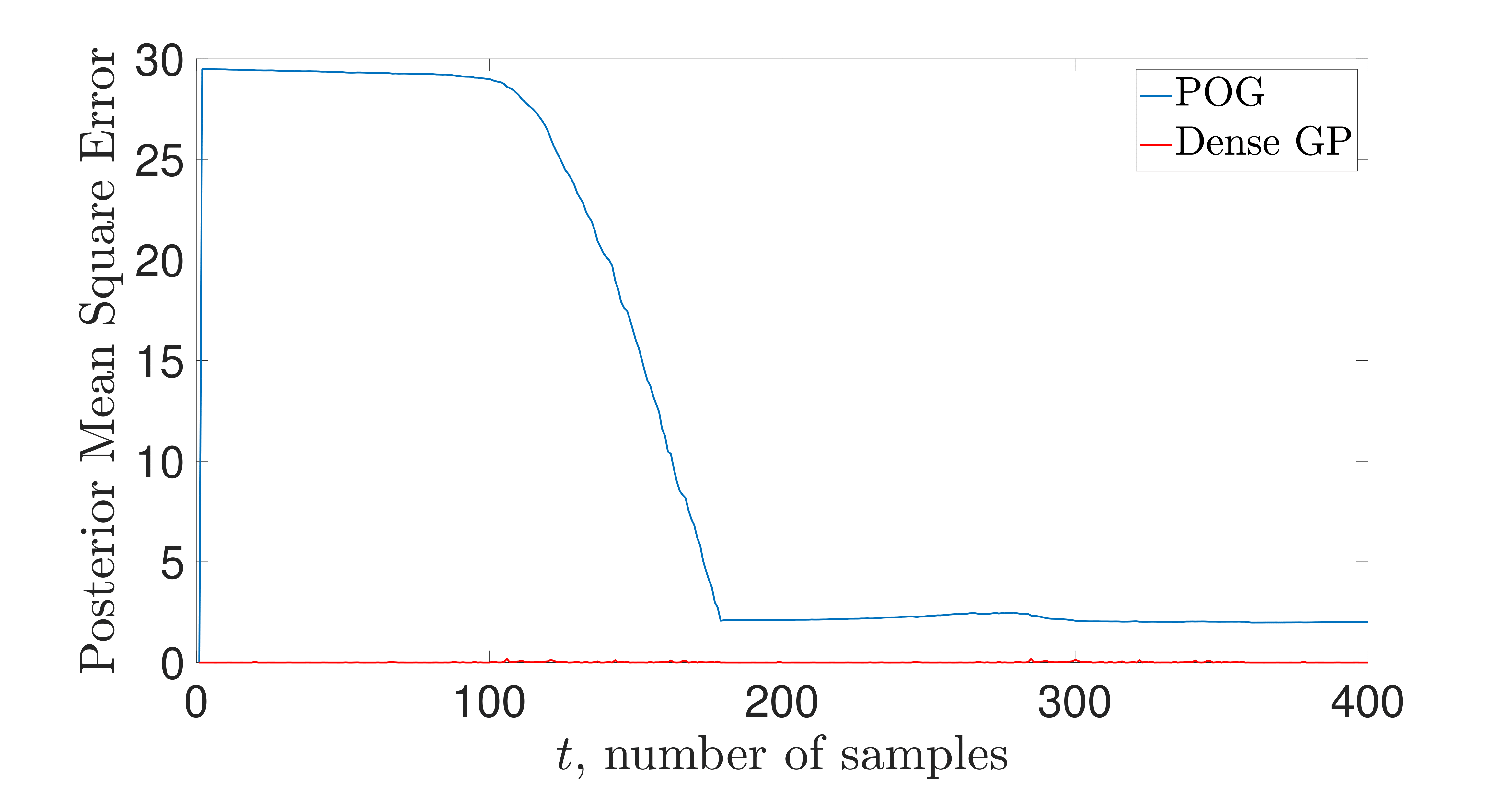
A. Koppel , "Consistent Online Gaussian Process Regression Without the
Sample Complexity
Bottleneck,"in IEEE American Control Conference (ACC) (to appear),
Philadelphia, PA, Jul. 10-12, 2019.
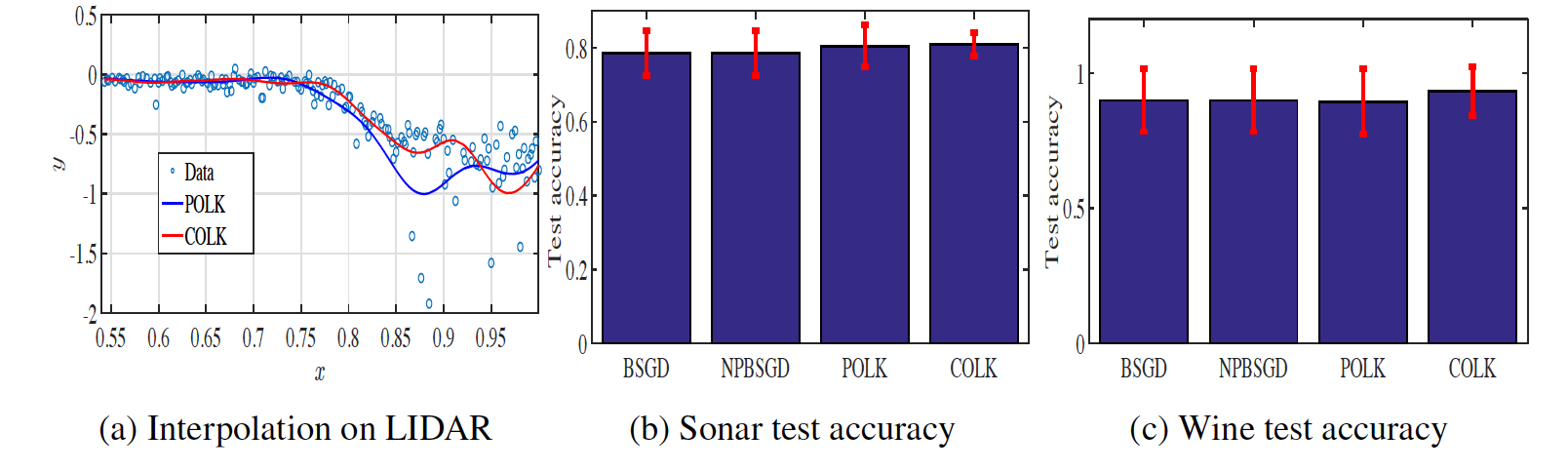
Results on a simple LIDAR nonlinear online regression data set are
shown to the right. Note that the number of points (pseudo-inputs) that
parameterizes the GP adapts online to whatever is needed for ensuring
we are near statistical consistency. This is done via the compression
routine based on the Hellinger metric. The statistical performance of
the compressed GP is fairly close to the dense one in terms of one-step
evolution with respect to the Hellinger metric, and this translates to
similar regression performance. Additional experimentation is ongoing.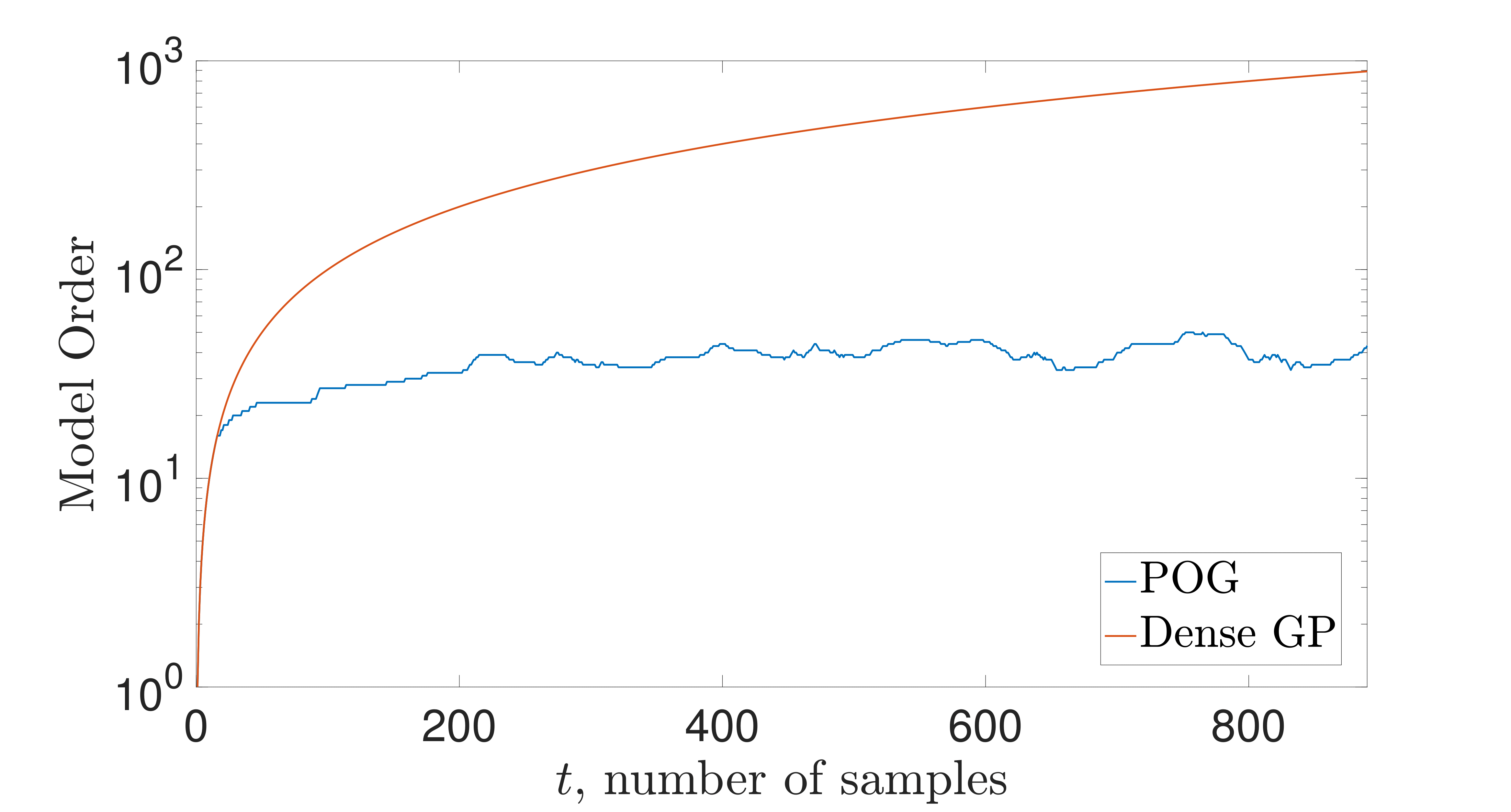
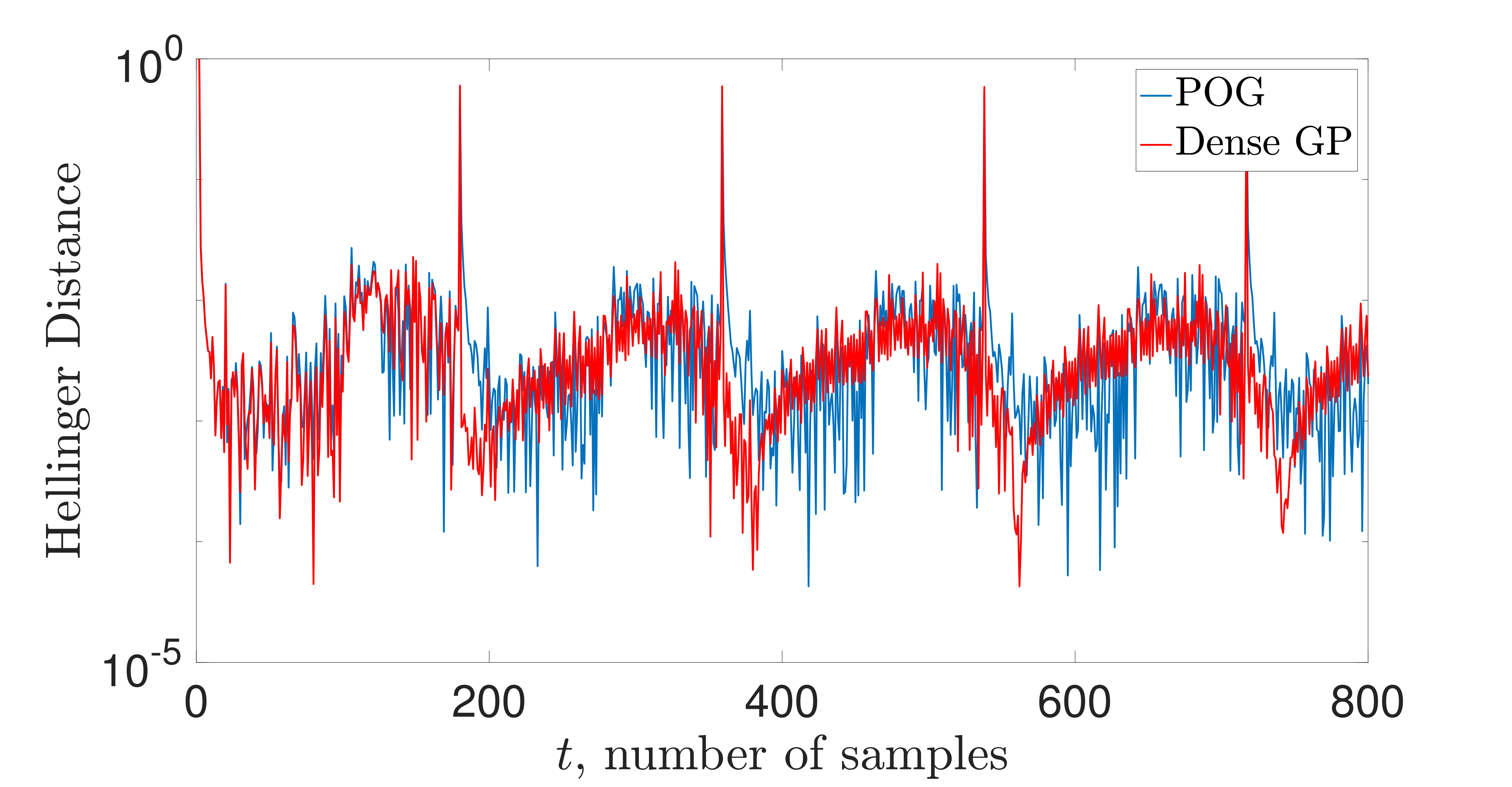
The key insight of this work is that one my greedily compress with
respect to a metric with a fixed approximation error, and then attain
convergence to a neighborhood that depends on this error. This is the
case in POLK (explained in earlier sections). This is true independent
of the choice of metric and the online learning algorithm to which it
is applied. Thus, in ongoing work, I am exploring how this idea may be
used to discern what is a near-optimal but finite number of particles
required to represent an arbitrary posterior distribution, not one that
is required to be Gaussian.
Machine learning problems such as, e.g., regression, classification, clustering, principal components, matrix completion, require solving optimization problems where the cost is a sum of a large number of individual costs, each of which denotes the model fitness at a current training example. Creating computationally efficient routines for such optimization problems has been the focus of much research over the past decades. Two major themes have emerged for how to manage the computational cost of solving such problems: stochastic/online approximation, i.e., cycling through subsets of data per model update, rather than full training sets, and decentralization.
Decentralization refers to splitting training sets over subsets of computational processors in order to alleviate the bottleneck in the training sample size, and also to attain benefits of parallel processing. Efforts to combine these approaches are referred to as decentralized stochastic (online) optimization.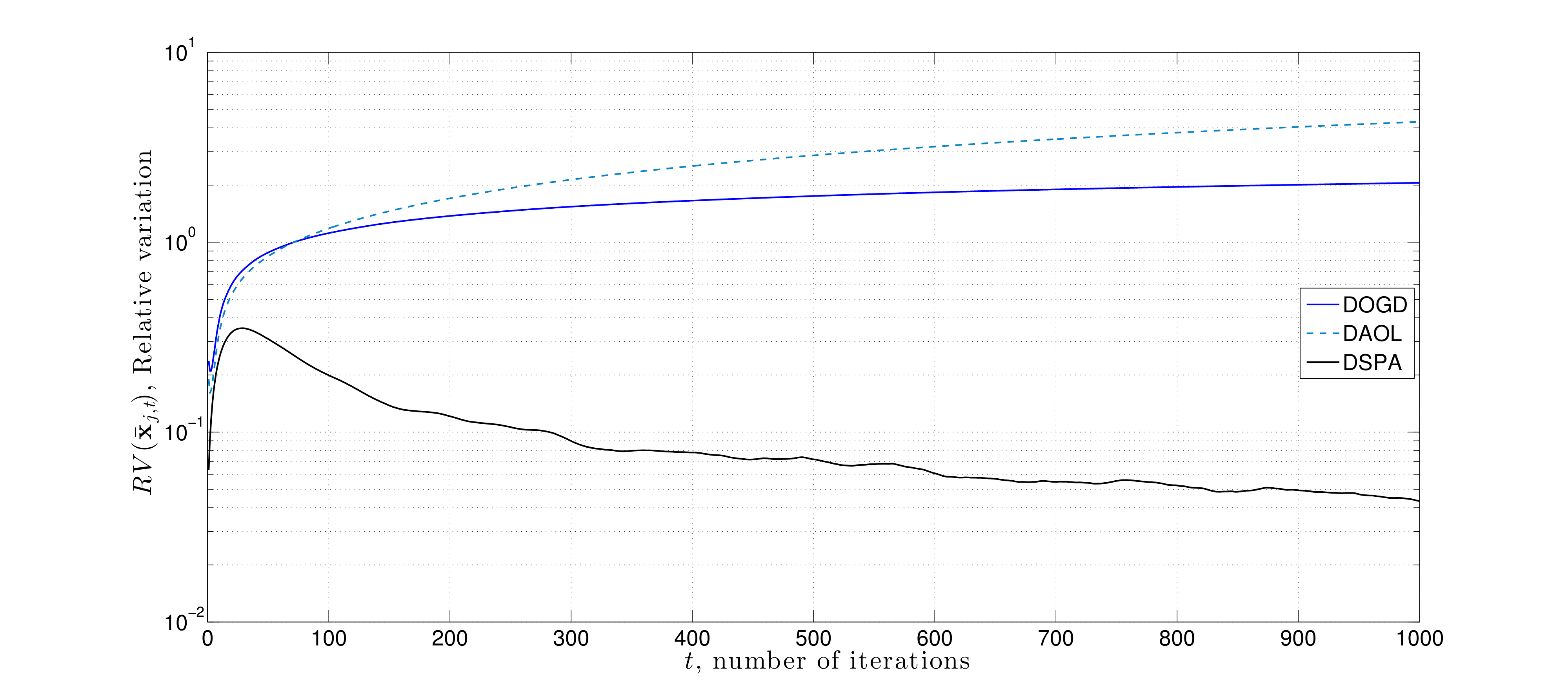
Through appropriate information mixing strategies, individual nodes may learn a decision variable which is optimal in terms of observations aggregated globally over the network.
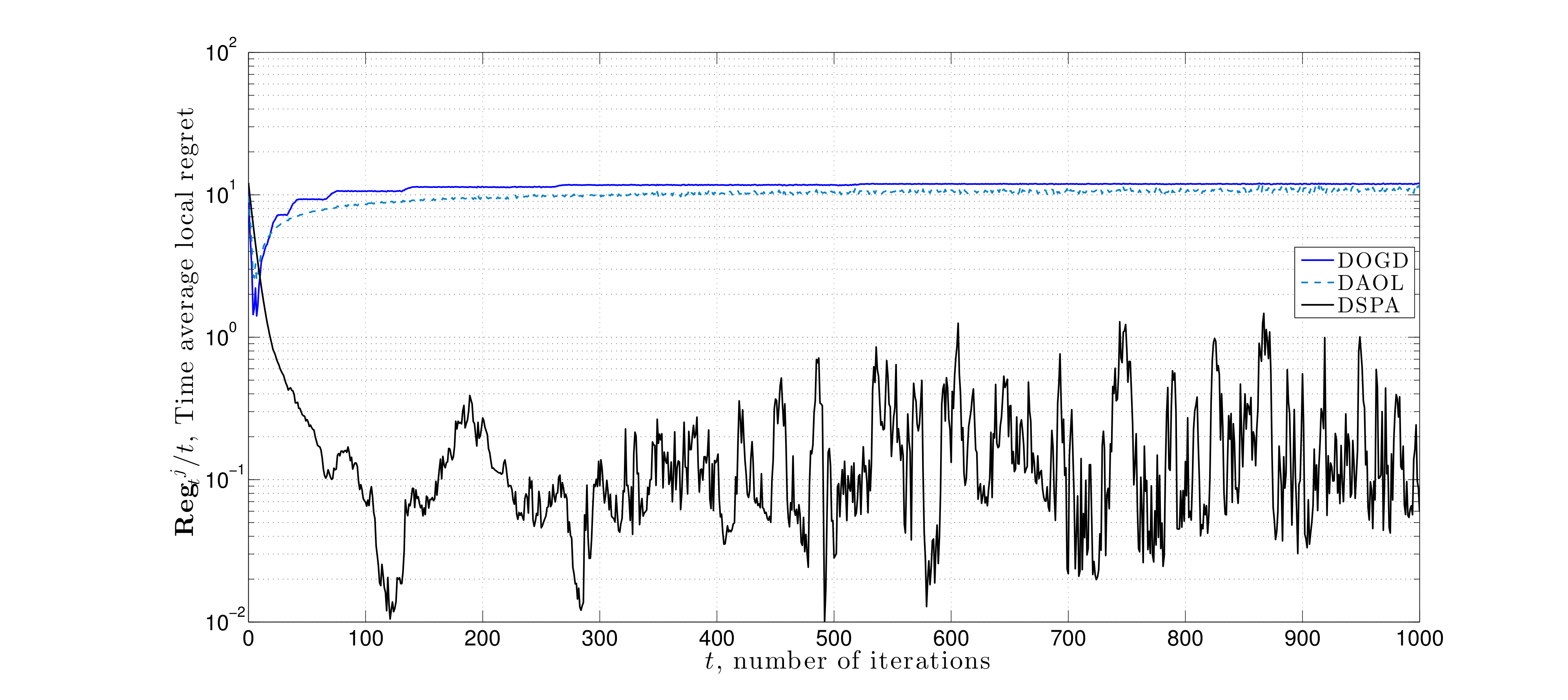
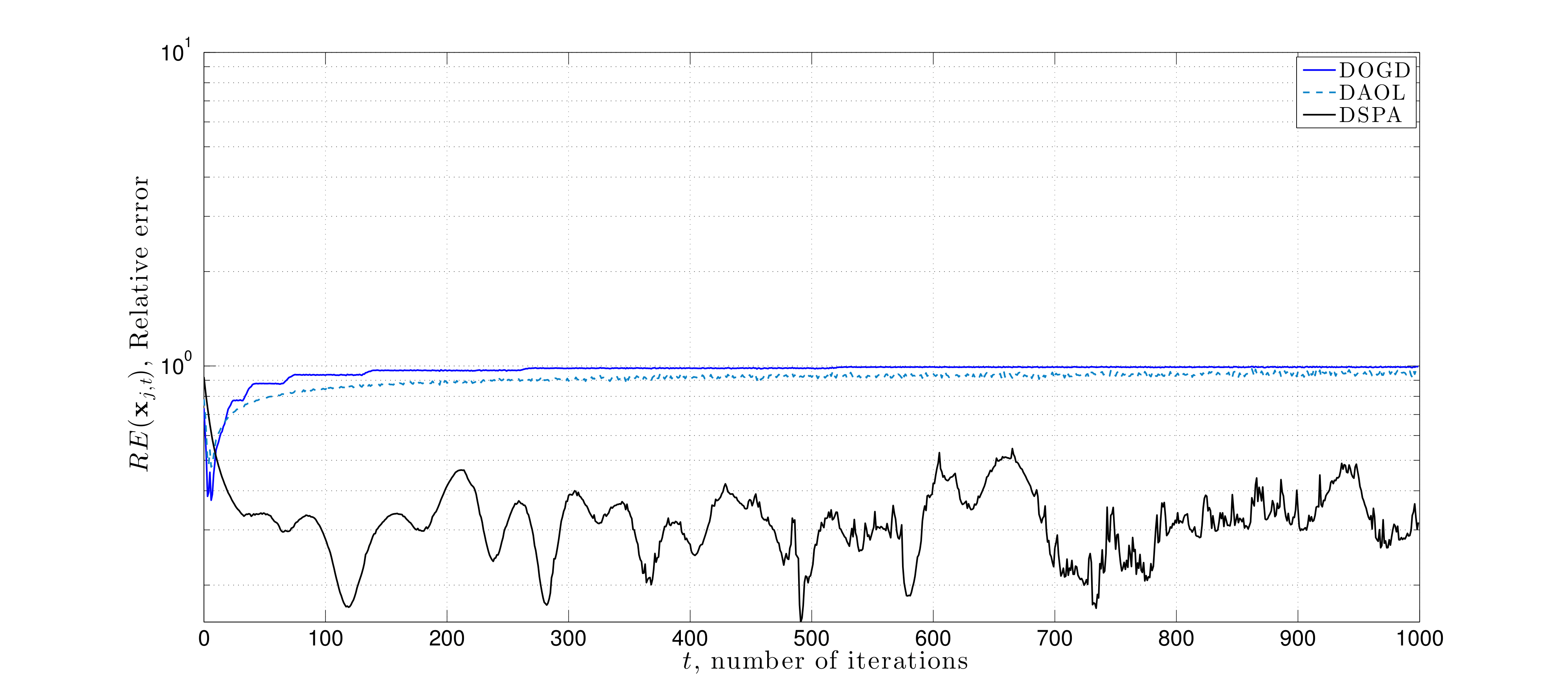
Prior approaches for decentralized information mixing were based upon schemes where agents combine a weighted average of neighbors decision variables with a local gradient step ("the consensus protocol"). By contrast, we propose new information mixing strategies, which employs duality in convex optimization to have agents approximately enforce local agreement constraints while learning based upon local information. Specifically, we use primal-dual (distributed saddle point), to solve decentralized online optimization problems and demonstrate their improvement over consensus methods for problems in which there is local heterogeneity in data across the network. The figures to the right demonstrate the improvement of saddle point method over consensus protocol (distributed gradient descent) for such problems on a grid network for solving distributed online linear regression. See [Video] for a presentation of this work:
A. Koppel, F. Jakubeic, and A. Ribeiro, “A saddle point algorithm for networked online convex optimization,” in IEEE Trans. Signal Process., Oct 2015.
Beyond Linear Statistical ModelsThe preceding discussion restricted focus to the case where the instantaneous cost of each computing node is assumed to be convex, and the constraint imposed by decentralization is that different nodes' decisions must coincide at optimality. In follow up work, we relaxed the convexity assumption so that individual nodes can learn more general decision variables defined by sparse feature approximations, i..e., supervised dictionary learning. The primary motivation for focusing on this development is to create a framework for autonomous terrain classification among a network of robots. See the following work for further details.
A. Koppel, G. Warnell, E. Stump, and A. Ribeiro, "D4L: Decentralized Dynamic Discrminative Dictionary Learning," in IEEE Trans. Signal and Info. Process over Networks, Feb. 2017.
Proximity without Consensus In distributed optimization problems, agent agreement may not always be the primary goal. In large-scale settings where one aims to leverage parallel processing architectures to alleviate computational bottlenecks, agreement constraints are suitable. In contrast, if there are different priors on information received at distinct subsets of agents, then requiring the network to reach a common decision may to degrade local predictive accuracy. Specifically, if the observations at each node are independent but not identically distributed, consensus yields the wrong solution. Moreover, there are tradeoffs in complexity and communications, and it may be that only a subset of nodes requires a solution.
In this work, we formulate a generalization of the usual decentralized optimization problem to the case where nodes are incentivized to select decisions that are nearby but not necessarily equal through the use of network proximity constraints. To solve this problem, we propose a stochastic variant of primal-dual method, and establish that it converges in expectation to a primal-dual optimal pair of this problem when a constant algorithm step-size is chosen. This work is summarized in the following journal paper:
A. Koppel, B. Sadler, and A. Ribeiro, ”Proximity without Consensus in Online Multi-Agent
Optimization,” in IEEE Trans. Signal Proc, Volume: 65 Issue: 12 , Page 3062-3077, June
15, 2017.
Here we consider a numerical experiment on a source localization problem where distinct nodes of a network sequentially observe noisy-perturbed range measurements. The noise is correlated with the node's distance to the source signal. Each node tries to estimate the source signal through either saddle point method with consensus constraints, distributed online gradient descent, or the saddle point method proposed here that uses proximity constraints. We observe that the later approach yields minimal estimation error.